Les graphiques (3): les données sur une longue période

En cette nouvelle année, je vais poursuivre ma série sur les graphiques par un sujet pas trop compliqué, les longues séries de données. Ces séries ont souvent comme caractéristique de prendre une forme trompeuse, parfois exponentielle. Pour pouvoir illustrer cette caractéristique, j’ai choisi des données canadiennes plutôt que québécoises, car les séries de données disponibles sont plus longues pour le Canada que pour le Québec.

Forme exponentielle

Dans le graphique qui suit, qui représente l’évolution de l’indice des prix à la consommation (IPC) au Canada depuis 1914, on a l’impression que l’IPC a peu augmenté jusque dans les années 1970, qu’il a soudain augmenté en flèche jusqu’au milieu des années 1980, a augmenté à peine un peu moins vite jusqu’au milieu des années 1990 et que son augmentation a ralenti quelque peu par la suite.

Il est possible de mieux rendre la présentation de l’évolution de longues séries du genre de différentes façons. On peut par exemple utiliser une échelle logarithmique ou plus simplement présenter le taux de croissance, dans le cas présent, le taux d’inflation. Personnellement, je n’aime pas utiliser des échelles logarithmiques, car on risque de confondre encore plus le lecteur. Allons-y donc avec le taux de croissance.

Sur le graphique qui suit, on peut voir que, contrairement à l’impression qu’on pouvait avoir en regardant le graphique précédent, l’inflation la plus forte au cours de ces presque 100 ans a eu lieu dans les premières années de la série, période qui fut suivie par une longue période de déflation (avant et après la grande crise de 1929). Comme on l’avait vu dans le graphique précédent, les années 1970 se sont caractérisées par une inflation assez forte et prolongée (stagflation), mais la baisse du taux d’inflation dans les années 1980 et surtout depuis les années 1990 fut beaucoup plus importante que le graphique précédent le laissait penser.

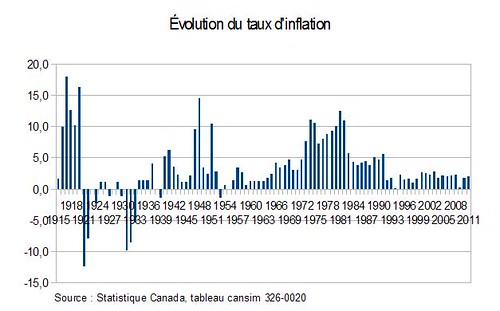
Tout cela peut sembler évident aux habitués des graphiques, mais j’ai vu tellement de personnes tomber dans le piège de la pente quasiment nulle au début des longues séries qu’il valait peut-être la peine d’en parler.

Forme quasi linéaire

La compréhension d’un graphique quasi linéaire de longue période peut présenter le même danger de fausse interprétation. Par exemple, en regardant le graphique qui suit, on a l’impression que l’évolution de la croissance du PIB canadien réel (après inflation) est bien linéaire, si ce n’est de petits ralentissements lors des récessions des débuts des années 1980 et 1990 et de la fin de la dernière décennie.

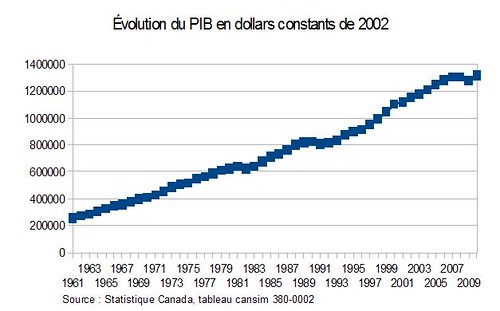
En transformant les données en taux de croissance, se dessine un portrait passablement différent. On voit bien dans le graphique suivant que la croissance la plus forte s’est réalisée en début de période. Par contre, les mouvements parfois très forts à la hausse et à la baisse d’une année à l’autre nous empêchent de se faire une idée claire de cette évolution.

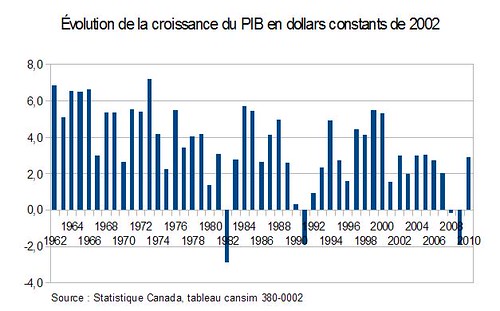
Dans un tel cas, il peut alors être plus éclairant de regrouper un peu ces données par période un peu plus longues pour voir si une tendance ne se dégage pas. C’est ce que j’ai fait dans le graphique suivant, en calculant les taux moyens de croissance annuelle du PIB par décennie :

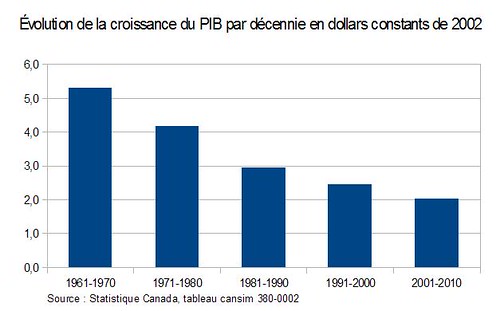
Là, la tendance est claire et nette! On s’aperçoit que le taux de croissance annuel moyen du PIB réel au Canada a diminué à chaque décennie depuis les années 1960.

Et ensuite…

Une fois les graphiques adaptés pour mieux voir les tendances, il reste à les interpréter. Pourquoi cette baisse depuis les années 1960? D’une part il faudrait vérifier si cette baisse n’est pas due à une variation dans la croissance de la population (en utilisant la croissance du PIB par habitant), à un changement dans la structure d’âge (calculer le ratio de dépendance démographique, par exemple), se poser des questions sur les conséquences de la définition du PIB et de ses lacunes, etc.

Même si une telle analyse serait intéressante, ce n’est pas l’objet de ce billet!  L’important ici est de réaliser qu’un graphique, aussi bien fait soit-il, ne donne pas toutes les réponses…