Les graphiques (5): les graphiques à deux axes – données de natures différentes

Je reprends ici ma série sur les graphiques. La dernière fois, on a vu qu’on pouvait appliquer des règles assez simples (enfin, presque simples!) pour présenter adéquatement les graphiques à deux axes qui regroupent des données du même type. Malheureusement, il n’est pas possible de faire la même chose avec des graphiques à deux axes qui présentent des données de natures différentes.

Pas de règles

Comme je l’avais mentionné dans les commentaires du dernier billet, je vais ici donner un exemple tiré d’une demande qui m’a été faite par Éric Pineault. Il m’a soumis ce graphique non tronqué :

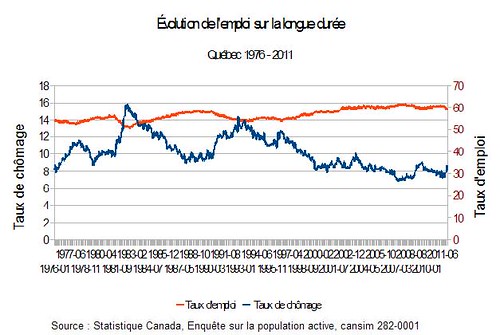
La façon de présenter un graphique dépend de notre objectif et de ce qu’on veut montrer. Ici, on voit bien les mouvements du taux de chômage, mais tout ce qu’on voit du taux d’emploi, c’est qu’il a monté, surtout depuis l’après récession des années 1990 et qu’il semble assez stable depuis le début des années 2000. Je lui ai plutôt proposé de le présenter ainsi :

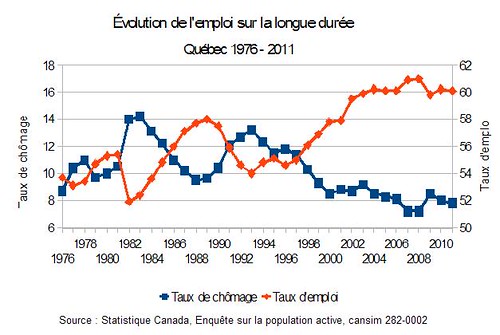
Là, on voit bien l’effet miroir entre ces deux données : quand le taux de chômage augmente, le taux d’emploi diminue et vice versa. On voit aussi que le niveau de long terme du taux d’emploi est beaucoup plus élevé depuis une dizaine d’années et le taux de chômage plus bas. La relation entre les taux d’emploi et de chômage me semble aussi bien plus claire.

J’ai en outre utilisé des moyennes annuelles plutôt que des données mensuelles en raison de la marge d’erreur très grande des données mensuelles de l’Enquête sur la population active (EPA), marge d’erreur à 95 % qui s’élève à 130 200 emplois, tandis qu’elle ne s’élève qu’à 45 300 (c’est quand même pas mal!) avec les données annuelles. Finalement, j’ai choisi de garder une différence de 12 points de pourcentage entre les valeurs du taux de chômage et du taux d’emploi pour que les mouvements des données soient comparables. Il s’agit en fait d’une décision un peu arbitraire, car ces deux taux ne sont pas compatibles, le dénominateur n’étant pas le même. En effet, le taux de chômage représente le nombre de chômeurs sur la population active et le taux d’emploi le nombre de personnes en emploi sur la population adulte (15 ans et plus).

Bref, les principes qu’on peut ou doit adopter dans la construction de ce genre de graphique varient énormément selon la nature des données qu’on compare et la relation qu’on veut illustrer avec son graphique. Le lecteur doit donc être très vigilant face à ces graphiques.

Corrélation et causalité

Bien souvent, l’idée le présenter un graphique à deux axes avec des données de natures différentes est de montrer que deux facteurs sont liés. C’est en fait là, bien plus que dans le jeu des échelles et du tronquage, que se trouvent les pièges dont il faut le plus se méfier.

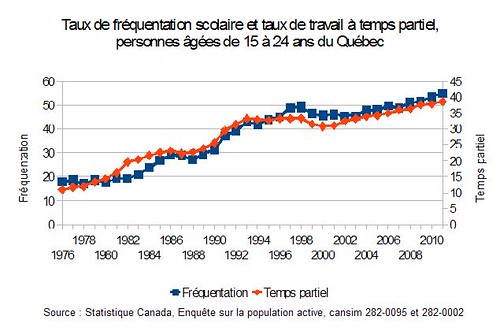
Le graphique qui suit montre la très forte corrélation (0,97, ce qui est énorme) entre le taux de travail à temps partiel des jeunes (15 à 24 ans) et leur taux de fréquentation scolaire à temps plein. Ce graphique laisse penser que la forte hausse du travail à temps partiel chez les jeunes serait causée en premier lieu par la hausse, toute aussi forte, de leur taux de fréquentation scolaire à temps plein. Mais la relation est-elle bien causale? Il est clair selon moi que les liens entre les deux sont logiques. Mais, il est toujours mieux de vérifier.

Pour ce, on peut par exemple regarder l’évolution du travail à temps partiel chez les étudiants à temps plein et les non-étudiants. Voici ce que ça donne :

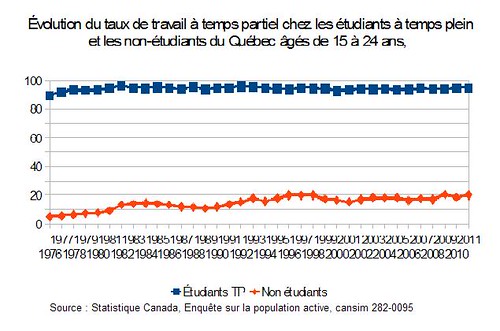
Sur ce graphique, on peut voir que le taux de travail à temps partiel a augmenté en début de période à la fois chez les étudiants à temps plein et les non étudiants, mais qu’il est resté relativement stable par la suite. La hausse du début de période se voit d’ailleurs dans le graphique précédent, car la ligne rouge du taux de travail à temps partiel passe de sous la courbe bleue (fréquentation scolaire) en 1976 à au-dessus vers 1982. Pour le reste, la relation semble bel et bien causale.

En fait, un autre phénomène explique la montée du travail à temps partiel chez les jeunes. Il s’agit de la forte hausse du taux d’emploi des jeunes étudiants à temps plein, qui est passé de 16 % en 1976 à 42 % en 2011 (je laisse le soin aux chercheurs de l’IRIS de faire le lien entre les droits de scolarité et cette hausse…), tandis que le taux d’emploi des non-étudiants a beaucoup moins augmenté (67 % en 1976 à 74 % en 2011, hausse observée presque uniquement chez les jeunes femmes).

Mais, il n’est pas toujours aussi facile de déterminer si une corrélation est causale. Parfois, on peut même avoir de la difficulté à différencier la cause de l’effet. Il existe toutefois des relations non causales plus faciles à trouver, comme dans le graphique qui suit, qui provient d’une page Internet très sérieuse que je vous invite à lire… Vous verrez que la cause de deux variables corrélées est souvent un troisième facteur… ou le hasard!

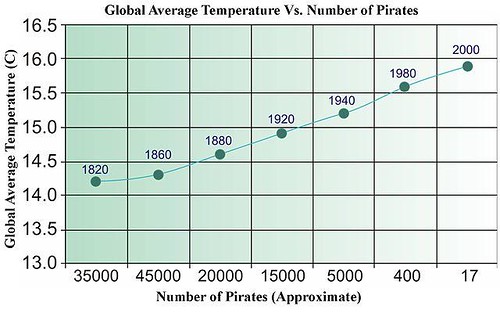
Comme ce graphique est en anglais et est très, très mal conçu (y a-t-il une corrélation ou une cause entre ces deux observations?), je l’ai refait!

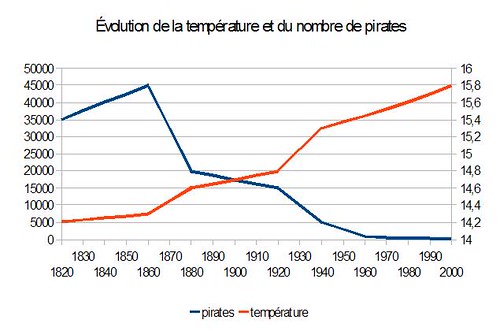
On voit bien la forte corrélation négative (-0,95 !). Mais, la baisse du nombre de pirates peut-elle vraiment influencer le climat (ou vice-versa)? D’ailleurs, l’auteur de cette blague a dû redoubler d’effort pour expliquer que le réchauffement s’est poursuivi lorsque le nombre de pirates a recommencé à croître…

« En 2008, Henderson interpréta l’accroissement de la piraterie dans le Golfe d’Aden comme une preuve supplémentaire car la Somalie a le nombre le plus élevé de pirates et les plus basses émissions de gaz à effet de serre de tous les pays »

Il n’y a rien à son épreuve!

Bon…

Cet exemple ridicule montre bien qu’il faut être vigilant avant de gober une relation de cause à effet pour la seule raison que deux facteurs sont corrélés. Je vous invite d’ailleurs à fournir aux lecteurs de ce blogue des exemples de graphiques qui tentent de nous faire avaler des couleuvres un peu moins évidentes. Je vous remercie à l’avance, en espérant que ce remerciement soit corrélé avec votre participation, et même causée par lui!