Les graphiques (4): les graphiques à deux axes – données de même type

Pour ce quatrième billet de ma série sur les graphiques, j’aborderai aujourd’hui la forme de graphique qui est la plus pratique pour mêler et influencer malicieusement un lecteur, soit les graphiques à deux axes. Je compte écrire deux billets sur cette forme de graphique en commençant par la moins perverse, soit celle qui regroupe des données du même type.

Un est tronqué, pas l’autre…

En cherchant tout autre chose, je suis tombé sur un graphique douteux à la page 8 de ce document de la Fédération des chambres de commerce du Québec (FCCQ), graphique que je reproduis ci-après :

Joli, non ? On compare ici l’évolution du nombre de faillites au Québec et au Canada, mais, pour accentuer visuellement l’importance relative de la baisse du nombre de faillites au Canada, on a pris soin de tronquer l’échelle de l’axe du Canada, sans le faire pour l’axe du Québec. Voici ce qu’aurait donné le même graphique sans le tronquer :

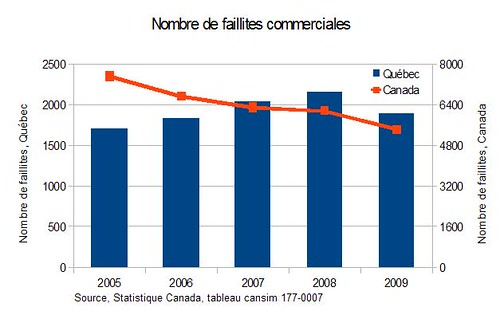
C’est moins spectaculaire comme ça! En fait, la FCCQ aurait pu simplement montrer que le pourcentage des faillites canadiennes au Québec est passé de 23 % en 2005 à 35 % en 2009, mais, bon c’est son choix! Et elle aurait pu aussi parler de la valeur monétaire de ces faillites, qui a atteint 48 % du total canadien en 2005, mais seulement 13 % en 2007 (les données pour 2008 et 2009 ne sont pas encore disponibles)! Mais cela aurait peut-être moins bien appuyé ses propos…

Peut-on tronquer un graphique à deux axes?

Pour illustrer cette section, je vais utiliser des données sur le taux d’emploi chez les jeunes étudiants à temps plein au Québec. Un graphique simple donne ce qui suit :

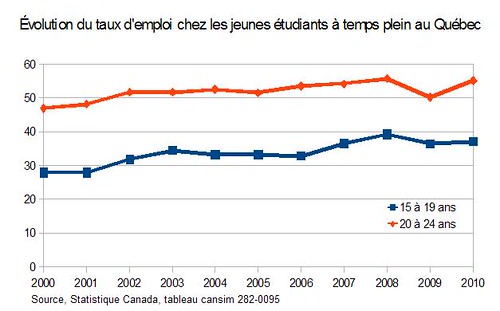
Ce graphique permet de voir que le taux d’emploi des jeunes étudiants à temps plein des deux groupes d’âge a augmenté au cours des 10 dernières années. Mais lequel de ces deux groupes a le plus augmenté? Difficile à dire… Essayons un graphique à deux axes :

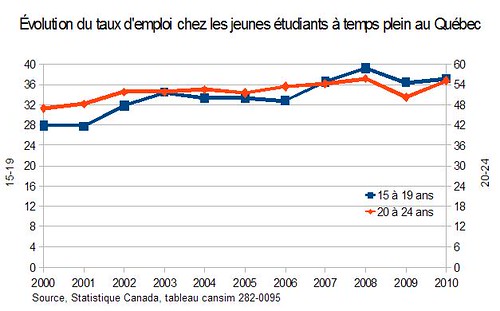
Ce n’est pas vraiment mieux. Un peu quand même car on voit que la ligne des 15-19 part plus bas que celle des 20-24. La croissance de leur taux d’emploi doit être plus grande.

Mais, on ne voit pas bien. Alors tronquons! Mais comment? Là, il y des règles à suivre. Voici ce que ça donne quand on veut seulement que les lignes partent et arrivent au même endroit :

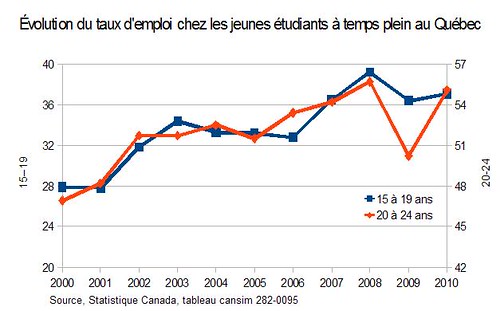
Ça, on voit mieux, mais les deux taux d’augmentation ont l’air identiques, même que celui des 20-24 a l’air plus fort, puisqu’il part en bas de celui des 15-19 et arrive au même endroit. Le problème est que la proportion entre le début et la fin de l’échelle n’est pas la même. Du côté des 15-19, à gauche, l’échelle passe de 20 à 40, soit du simple au double. Par contre, du côté des 20-24, à droite, elle passe de 42 à 57, soit beaucoup moins que le double (57/42 = 1,37).

Pour faire un graphique à deux axes avec des échelles tronquées, il faut que la proportion entre le bas et le haut de l’échelle soit la même, sinon on «avantagera» immanquablement une série de données par rapport à l’autre.

Il faut en plus autant que possible choisir les échelles pour que soit le début, soit la fin des lignes arrivent à peu près au même endroit, ou encore que les lignes se croisent, sinon les taux respectifs d’augmentation ne seront pas visualisés correctement et, encore là, une série sera «avantagée» par rapport à l’autre. Voici un graphique qui respecte ces deux règles :

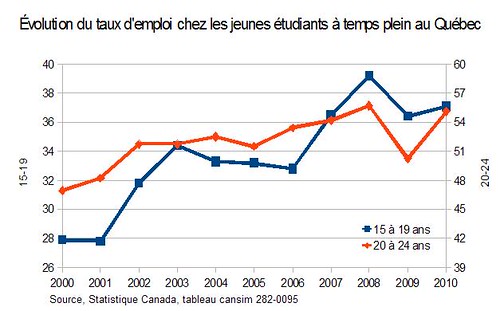
La première règle, qui veut que les proportions entre le bas et le haut des échelles des deux axes soit égales est respectée, puisque 26/40 = 39/60 = 0,65. La deuxième aussi puisque les deux lignes se croisent et arrivent à peu près au même endroit. On voit ici clairement que le taux d’emploi des 15-19 a augmenté plus fortement que celui des 20-24 et à quel moment les taux d’augmentation ont différé ou pas. Notre objectif est donc atteint…

Mais, est-ce nécessaire?

Personnellement, j’évite comme la peste ce genre de graphique. Si le résultat est intéressant, il n’est pas évident à interpréter. J’ai en fait écrit ce billet uniquement pour que le lecteur puisse vérifier si les deux règles sont respectées quand il croise ce genre de graphique sur Internet ou dans tout autre document. Et il verra qu’elles le sont rarement!

Ce que j’aurais fait? J’aurais laissé le graphique comme au début, ou l’aurais fait en ratio, pour bien faire ressortir la croissance plus forte chez les 15-19 :

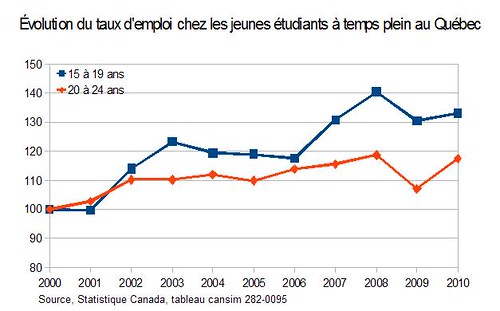
Trop simple…