Les graphiques (2): quelle croissance veut-on montrer?

Dans le premier billet sur les graphiques, on a vu qu’on peut très bien tronquer un graphique, c’est-à-dire ne pas faire partir l’axe des Y à 0, sans nécessairement tricher. Cette fois nous verrons un problème de confusion potentielle dans la présentation sur un même graphique d’éléments de dimensions différentes.

Croissance en points de pourcentages ou en proportion?

Quand on veut comparer des éléments de dimensions différentes, il peut arriver qu’on donne une impression fautive de l’évolution réelle de ces éléments. Par exemple, le graphique qui suit montre l’évolution du taux de fréquentation scolaire à temps plein des jeunes Québécois âgés de 15 à 19 ans, de 20 à 24 ans et de 25 à 29 ans.

À première vue, le taux de fréquentation scolaire des jeunes de 15 à 19 ans et celui des jeunes de 20 à 24 ans semble avoir augmenté à peu près au même rythme entre 1976 et 1997, puis s’être stabilisé par la suite, tandis qu’on dirait celui des jeunes de 25 à 29 ans a aussi augmenté, mais beaucoup moins. En effet, les deux courbes des plus jeunes ont une pente très semblable, tandis que celle des plus vieux est beaucoup moins abrupte.

En termes d’augmentation en points de pourcentage, cette perception est exacte, le taux de fréquentation de ces trois groupes ayant augmenté respectivement de 21, 23 et 5 points de pourcentage entre 1976 et 1997. Mais est-ce la même chose en proportion?

Pour le savoir, il est préférable de faire partir des trois groupes du même point, d’un ratio égal, comme on peut le voir sur le graphique suivant. Pour ce, il s’agit simplement de diviser chaque donnée annuelle par celle de l’année de départ (et de multiplier par 100, si on veut un ratio de départ de 100…). Voici le résultat :

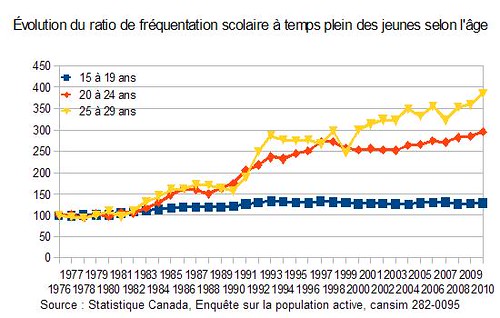
Ouf, ce n’est plus du tout la même chose! Le groupe du haut du premier graphique est maintenant en bas, et celui qui était en bas est en haut! Cette fois, ce sont les données des jeunes de 20 à 24 ans et 25 à 29 ans qui se suivent jusque vers la fin des années 1990. Par la suite, le taux de fréquentation scolaire des 20-24 se stabilise, tandis que celui des 25-29 continue à augmenter, phénomène qu’il était à peut près impossible de capter dans le graphique précédent.

Par contre, ce graphique aussi peut être trompeur. Le taux de fréquentation scolaire des 15-19 semble avoir peu augmenté, tandis qu’on a bien vu sur le graphique précédent que ce n’est pas le cas. Il est certain qu’il est impossible de faire doubler un taux de fréquentation scolaire qui était à 62 % au départ, tandis que de faire doubler un taux qui était à seulement 3 %, comme celui des 25-29 ans est plus «facile»! Mais il a presque quadruplé, ce qui est un phénomène de société tout de même digne de mention qui passait tout à fait inaperçu (sauf pour les lynx…) dans le premier graphique.

On peut aussi favoriser une présentation qui montre à la fois l’ampleur de l’augmentation du taux de fréquentation scolaire de chacune des tranches d’âge et le niveau de fréquentation. Comme ici :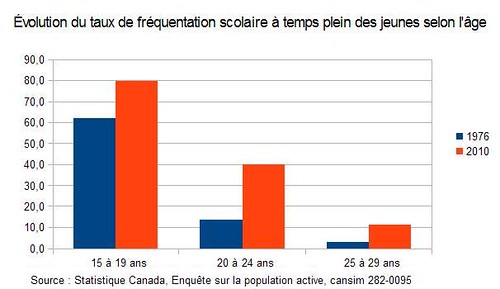

Dans ce graphique, on voit très bien les deux éléments que nous voulions montrer, mais on ne sait pas quand le changement s’est réalisé. Que voulez-vous, il n’y a rien de parfait dans ce bas monde… On ne sait pas que le gros de l’augmentation chez les 15-19 et les 20-24 s’est passée avant l’an 2000 et on ne sait pas non plus qu’elle s’est poursuivie sensiblement au même rythme chez les 25-29 entre le début des années 1980 et la fin de la première décennie des années 2000.

Que faire?

Tout dépend ce qu’on veut montrer. Par exemple, le premier graphique illustre bien la forte hausse du taux d’obtention du diplôme d’études secondaires des moins de 20 ans au cours de la période où le taux de fréquentation scolaire des 15-19 a augmenté, comme on peut le voir à la page 189 des indicateurs de l’éducation du ministère de l’Éducation, du Loisir et du Sport (MELS). On peut en effet observer que ce taux d’obtention est passé de 53,1 % en 1975-1976 à 73,8 % en 1995-1996, pour ensuite demeurer assez stable.

Le deuxième graphique, qui montre surtout la hausse du taux de fréquentation scolaire des 20-24 et des 25-29, lui, illustre à la fois l’augmentation spectaculaire du taux d’obtention du diplôme d’études secondaires chez les adultes de 20 ans et plus (de 4,1 % en 1975-1976 à 14,7 % en 1995-1996, et même jusqu’à 20,3 % en 2009-2010) qu’on peut voir à la même page 189, l’augmentation du taux d’obtention du diplôme d’études collégiales (de 22,2 % en 1975-1976 à 48,1 % en 2008-2009) qu’on peut voir à la page 200, et celui des trois diplômes universitaires qu’on peut voir à la page 204.

Pour éviter de tromper le lecteur, il est souvent bon de monter deux ou trois de ces graphiques, mais surtout de mentionner leurs pièges potentiels dans le texte d’accompagnement. Montrer ces trois graphiques est dans le fond le meilleur moyen pour visualiser les divers aspects d’un phénomène comme celui-là. Cela dit, autant que possible, il faut éviter de mettre sur un même graphique des éléments de dimensions aussi différentes.

Le graphique de la page 118 du même document du MELS montre très bien ce qu’il ne faut pas faire… Si vous êtes capable de voir la tendance précise de l’évolution de l’accès au doctorat, bravo!

Je poursuivrai cette série sur les pièges des graphiques sous peu… L’an prochain, disons!